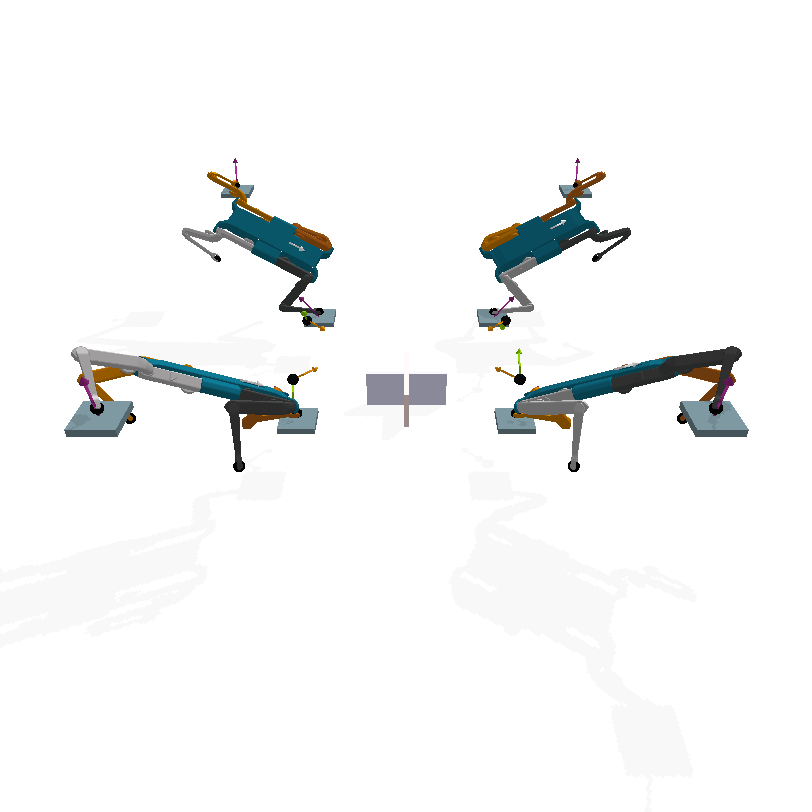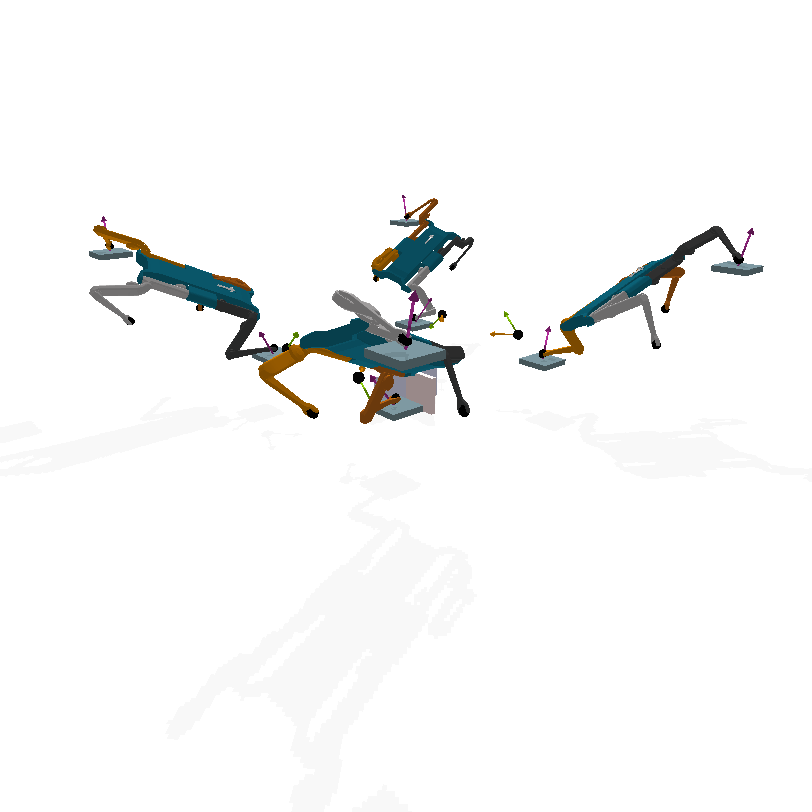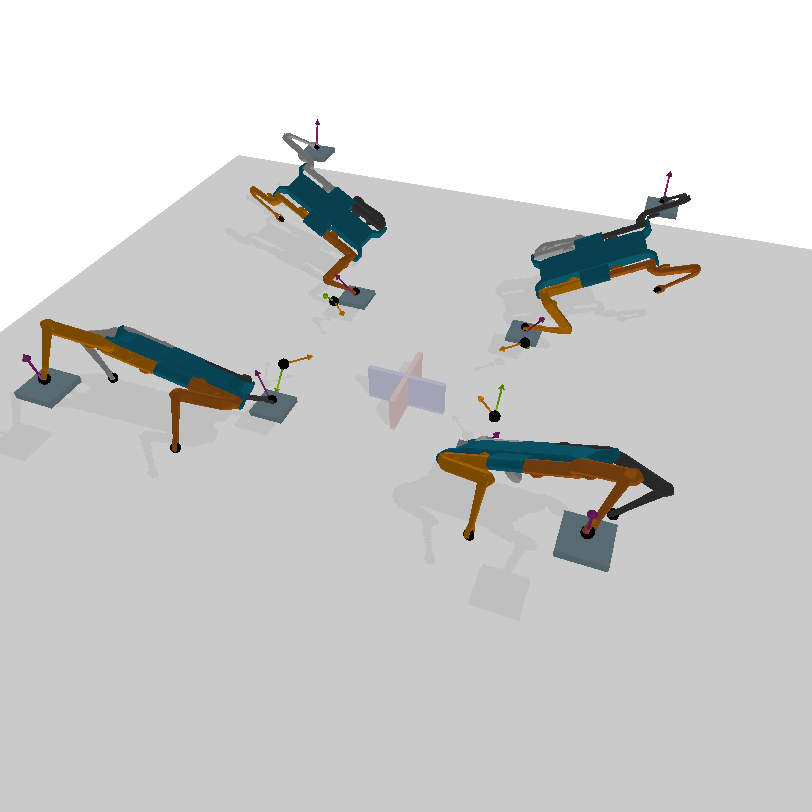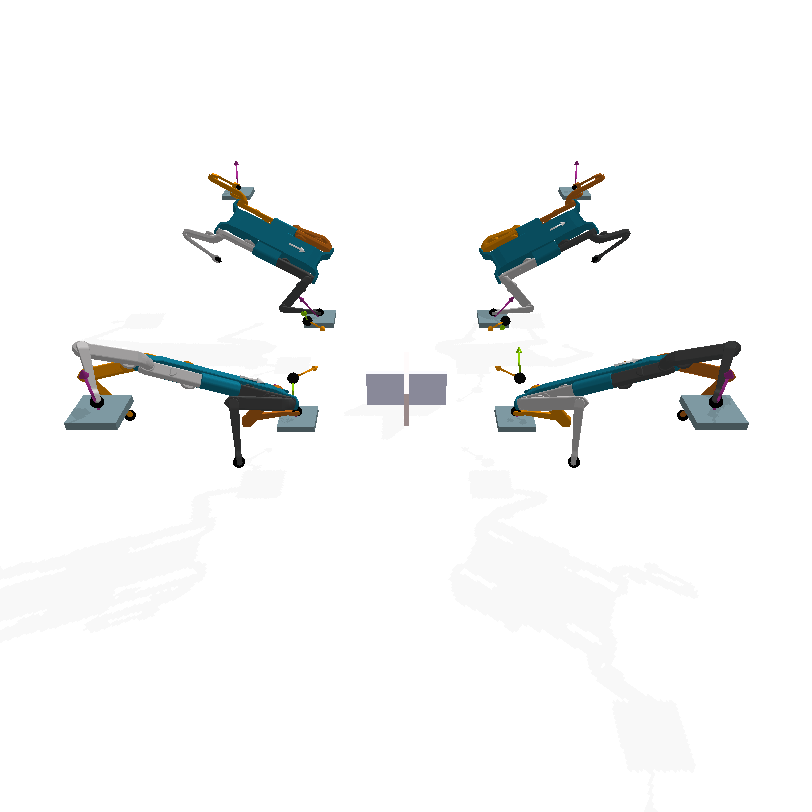On discrete symmetries of robotic systems: A data-driven and group-theoretic analysis

Daniel Ordoñez-Apraez٭☸, Mario Martin†, Antonio Agudo* Francesc Moreno-Noguer*
☸ Italian Institute of Technology, * Institut de Robòtica i Informàtica industrial IRI-CSIC, † Universitat Politècnica de Catalunya · Barcelona Tech - UPC
Robotics Science and Systems 2023
Paper Code

Abstract

We present a comprehensive study on discrete morphological symmetries of dynamical systems, which are commonly observed in biological and artificial locomoting systems, such as legged, swimming, and flying animals/robots/virtual characters. These symmetries arise from the presence of one or more planes/axis of symmetry in the system's morphology, resulting in harmonious duplication and distribution of body parts. Significantly, we characterize how morphological symmetries extend to symmetries in the system's dynamics, optimal control policies, and in all proprioceptive and exteroceptive measurements related to the system's dynamics evolution. In the context of data-driven methods, symmetry represents an inductive bias that justifies the use of data augmentation or symmetric function approximators. To tackle this, we present a theoretical and practical framework for identifying the system's morphological symmetry group $\G$ and characterizing the symmetries in proprioceptive and exteroceptive data measurements. We then exploit these symmetries using data augmentation and $\G$-equivariant neural networks. Our experiments on both synthetic and real-world applications provide empirical evidence of the advantageous outcomes resulting from the exploitation of these symmetries, including improved sample efficiency, enhanced generalization, and reduction of trainable parameters.

Video Presentation

Symmetries of robotic systems

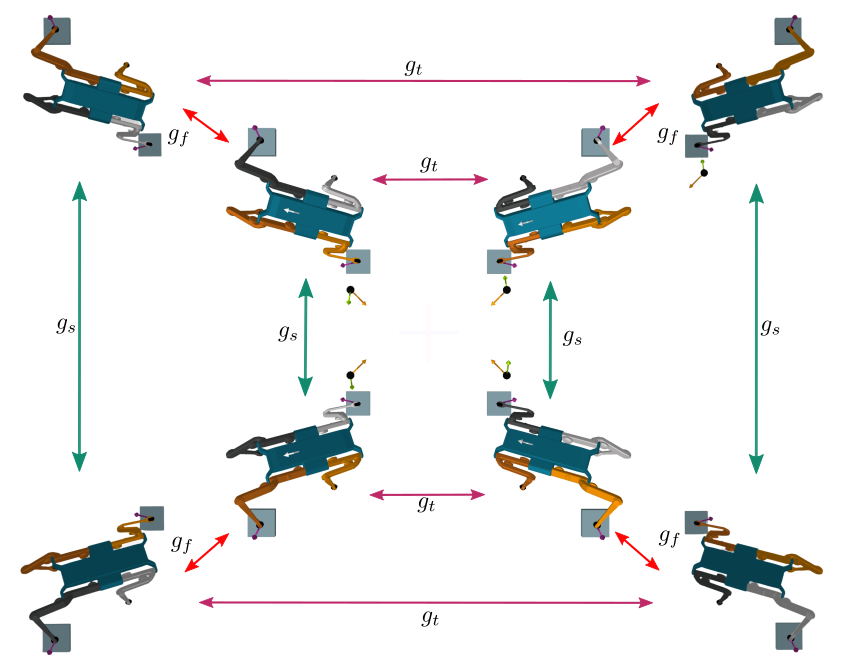
In the context of dynamical systems, a symmetry is a state transformation that results in another functionally equivalent state under the governing dynamics. This work particularly focuses Discrete Morphological Symmetries. Formally, these are discrete (or finite) symmetry groups that capture the equivariance of the robot’s dynamics, arising from the duplication of rigid bodies and kinematic chains. These symmetries are ubiquitous on biological and artificial locomoting systems, such as legged, swimming, and flying animals/robots/virtual characters. As an example consider the Mini-Cheetah robot, which has a C2xC2xC2 symmetry group, as shown in the figure below.

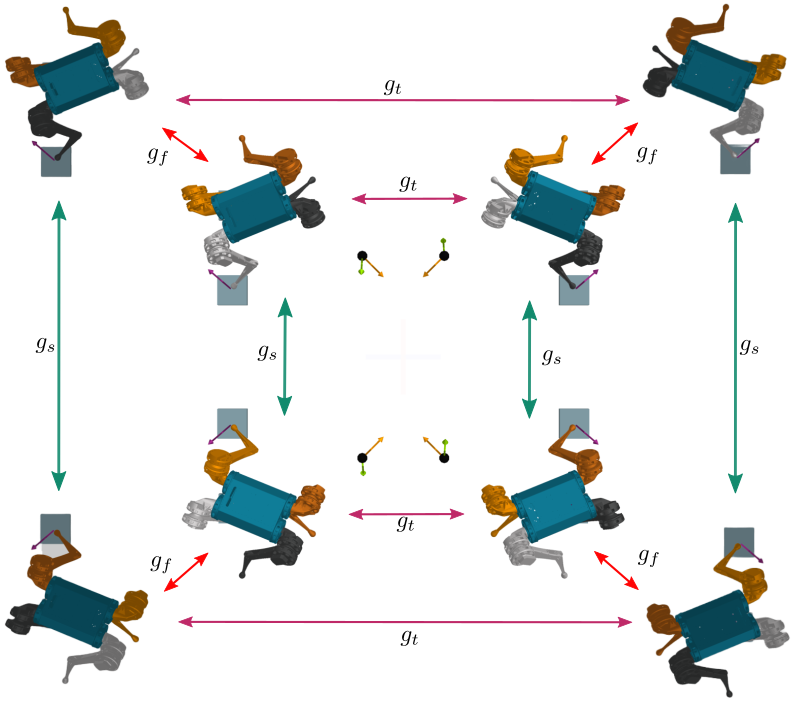
Morphological Symmetries Mini-Cheetah quadruped robot, Caley Diagram, Discrete Symmetry Group Morphological Symmetries Mini-Cheetah quadruped robot, State symmetry, Discrete Symmetry Group

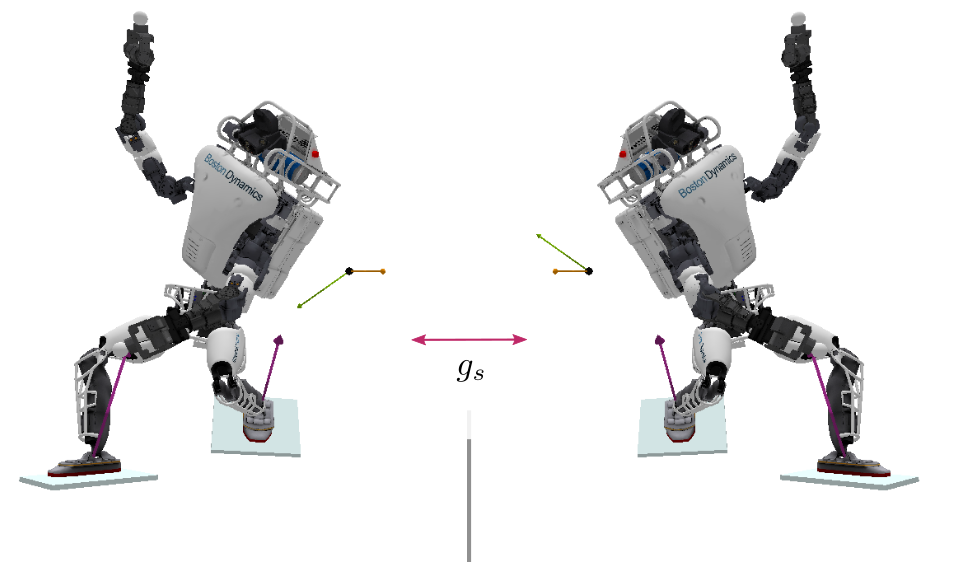
Symmetries provide a valuable geometric bias, as modeling and controlling the dynamics of a single state suffices to identify and control the dynamics of all of its symmetric states:

Furthermore, symmetries also provide a valuable bias for data-driven applications as we can use techniques of data-augmentation to multiply the number of samples recorded from our robot operation by the number of symmetries of the system. Or we can use symmetric function approximators, such as equivariant neural networks, to address any learning problem involving proprioceptive or exteroceptive data measurements.

Caley Diagrams of Morphological Symmetries

Poster

BibTeX


@INPROCEEDINGS{Ordonez-Apraez-RSS-23,
AUTHOR    = {Daniel F Ordonez-Apraez AND Martin, Mario AND Antonio Agudo AND Francesc Moreno},
TITLE     = {{On discrete symmetries of robotics systems: A group-theoretic and data-driven analysis}},
BOOKTITLE = {Proceedings of Robotics: Science and Systems},
YEAR      = {2023},
ADDRESS   = {Daegu, Republic of Korea},
MONTH     = {July},
DOI       = {10.15607/RSS.2023.XIX.053}
}